عناصر رادیواکتیو و نیمه عمر آن ها
آذر 5, 1403
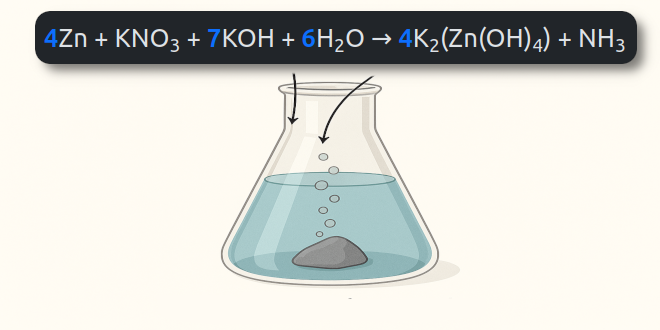
جداسازی ایزوتوپ های اورانیوم
دی 2, 1403انتگرال یک مفهوم اساسی در حساب دیفرانسیل و انتگرال است که با انباشت مقادیر در یک محدوده پیوسته سروکار دارد. این عمل معکوس تمایز است. آن را برخلاف یافتن شیب یک منحنی در نظر بگیرید. ادغام ناحیه زیر یک منحنی را پیدا می کند. دو نوع اصلی وجود دارد:
1. انتگرال معین:
• تعریف: انتگرال معین، مساحت *دقیق* را در زیر یک منحنی بین دو نقطه مشخص (محدودیت های یکپارچه سازی) محاسبه می کند.
• علامت گذاری:
∫ab f(x) dx
* ∫ نماد انتگرال است.
* مقادیر a و b حد پایین و بالای ادغام هستند (مقدار x تعیین کننده بازه).
* عبارت f(x) تابعی است که منحنی را نشان می دهد.
* عبارت dx نشان می دهد که ادغام با توجه به x است.
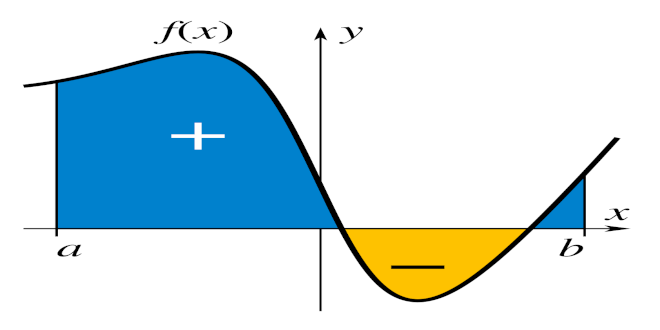
• تفسیر هندسی: انتگرال معین ناحیه علامت دار بین منحنی y = f(x)، محور x و خطوط عمودی x = a و x = b را نشان می دهد. نواحی زیر محور x منفی در نظر گرفته می شوند.
• محاسبه: انتگرال معین با استفاده از قضیه اساسی حساب دیفرانسیل و انتگرال محاسبه می شود که شامل یافتن یک پاد مشتق (برعکس مشتق) تابع و ارزیابی آن در مرزهای ادغام است. نتیجه عددی است که منطقه را نشان می دهد.
2. انتگرال نامعین:
• تعریف: انتگرال نامعین یک *خانواده* از توابع را پیدا می کند که مشتق آن تابع داده شده است. نشان دهنده ضد مشتق است.
• علامت گذاری:
∫ f(x) dx
* به عدم وجود محدودیت های ادغام توجه کنید.
• تفسیر هندسی: به طور مستقیم یک منطقه را نشان نمی دهد. در عوض، تابعی (به علاوه یک ثابت دلخواه) را نشان می دهد که شیب آن در هر نقطه x با f(x) داده می شود.
• محاسبه: انتگرال نامعین شامل یافتن تابع F(x) به گونه ای است که F'(x) = f(x). از آنجا که مشتق یک ثابت صفر است، انتگرال نامعین همیشه شامل یک ثابت دلخواه “+C” است.
مفاهیم و کاربردهای کلیدی:
• ضد مشتق: فرآیند یافتن انتگرال نامعین را ضد تمایز می گویند. این روند معکوس تمایز است.
• قضیه اساسی حساب دیفرانسیل و انتگرال: تمایز و ادغام را به هم متصل می کند و ابزار قدرتمندی برای محاسبه انتگرال های معین ارائه می دهد.
• برنامه ها: انتگرال ها کاربردهای فوق العاده گسترده ای در بسیاری از زمینه ها دارند، از جمله:
* فیزیک: محاسبه کار، جابجایی، و دیگر کمیت های فیزیکی.
* مهندسی: تعیین نواحی، حجم ها و مرکزها.
* احتمال و آمار: محاسبه احتمالات و مقادیر مورد انتظار.
* اقتصاد: یافتن کل هزینه، درآمد و سایر مقادیر اقتصادی.
در اصل، انتگرال یک ابزار قدرتمند برای انباشت مقادیر در محدوده های پیوسته است، که راهی برای حل مسائل مربوط به مناطق، حجم ها و بسیاری از کاربردهای دیگر در زمینه های مختلف ارائه می دهد. انتگرال معین یک پاسخ عددی (مساحت زیر منحنی) می دهد، در حالی که انتگرال نامعین یک تابع (ضد مشتق) ارائه می دهد.
کاربرد انتگرال در شیمی
انتگرال ها کاربردهای متعددی در شیمی دارند، عمدتاً در مناطقی که تغییرات مداوم و تجمع کمیت ها درگیر است. در اینجا چند مثال کلیدی آورده شده است:
1. سینتیک:
• قوانین نرخ: انتگرال ها برای استخراج قوانین نرخ یکپارچه از قوانین نرخ دیفرانسیل استفاده می شوند. قوانین سرعت دیفرانسیل سرعت لحظه ای یک واکنش را توصیف می کنند، در حالی که قوانین سرعت یکپارچه غلظت واکنش دهنده را به زمان مرتبط می کند. حل این موارد اغلب مستلزم ادغام است. برای مثال، ادغام قانون سرعت برای یک واکنش مرتبه اول، معادله غلظت واکنش دهنده را به عنوان تابعی از زمان به دست می دهد.
• نرخ واکنش: تعیین سرعت متوسط یک واکنش در یک بازه زمانی اغلب مستلزم محاسبه مساحت زیر منحنی غلظت در مقابل نمودار زمان است که با استفاده از یکپارچه سازی انجام می شود.
2. ترمودینامیک:
• کار و گرما: محاسبه کار انجام شده روی یا توسط یک سیستم یا گرمای منتقل شده در طول یک فرآیند اغلب مستلزم یکپارچگی است. به عنوان مثال، کار انجام شده در طول انبساط یا فشرده سازی یک گاز با ادغام رابطه فشار و حجم محاسبه می شود.
• انرژی آزاد گیبس: بسیاری از محاسبات ترمودینامیکی شامل ادغام کمیت های ترمودینامیکی مانند تغییرات انرژی آزاد گیبس در یک محدوده دما می باشد.
3. مکانیک کوانتومی:
• توابع موج: احتمال یافتن یک ذره در ناحیه خاصی از فضا با ادغام مجذور تابع موج بر روی آن ناحیه به دست می آید.
• سطوح انرژی: محاسبه سطوح انرژی اتم ها و مولکول ها اغلب شامل حل معادله شرودینگر است که اغلب مستلزم استفاده از انتگرال است.
4. طیف سنجی:
• شدت خط طیفی: تجزیه و تحلیل و تفسیر داده های طیفی گاهی شامل ادغام شدت اوج در طیف سنجی برای تعیین غلظت یک ماده است.
5. مکانیک آماری:
• توابع پارتیشن: محاسبه توابع پارتیشن، که توزیع سطوح انرژی در یک سیستم را توصیف می کند، شامل یکپارچه سازی بر روی حالت های قابل دسترسی است. این برای درک خواص ترمودینامیکی بسیار مهم است.
6. الکتروشیمی:
• جریان و شارژ: محاسبه کل بار عبور شده از یک سلول الکتروشیمیایی در طول زمان نیاز به یکپارچه سازی جریان در طول زمان دارد.
7. مهندسی شیمی:
• طراحی راکتور: مدل سازی و طراحی راکتورهای شیمیایی اغلب شامل حل معادلات دیفرانسیل است که نیاز به تکنیک های یکپارچه سازی دارند. تعیین مشخصات غلظت واکنش دهنده ها در یک راکتور یک مثال کلاسیک است.
• توازن جرم و انرژی: حل معادلات تراز جرم و انرژی برای فرآیندهای پیوسته اغلب نیاز به یکپارچه سازی دارد.
اینها تنها بخشی از برنامه های کاربردی هستند. هر زمان که با تغییرات مداوم یا انباشت مقادیر در سیستم های شیمیایی سر و کار دارید، احتمالاً انتگرال ها درگیر هستند. تکنیک های خاص مورد استفاده بسته به پیچیدگی مسئله متفاوت خواهد بود، اما حساب انتگرال چارچوب قدرتمندی برای مدل سازی و حل چنین مسائلی فراهم می کند.